|
|
@@ -0,0 +1,661 @@
|
|
|
+
|
|
|
+# #ifdef PRIMER_BOOK
|
|
|
+===== Example of Classes for Geometric Objects =====
|
|
|
+# #else
|
|
|
+======= Inner Workings of the Pysketcher Tool =======
|
|
|
+# #endif
|
|
|
+
|
|
|
+We shall now explain how we can, quite easily, realize software
|
|
|
+with the capabilities demonstrated above. Each object in the
|
|
|
+figure is represented as a class in a class hierarchy. Using
|
|
|
+inheritance, classes can inherit properties from parent classes
|
|
|
+and add new geometric features.
|
|
|
+
|
|
|
+# #ifndef PRIMER_BOOK
|
|
|
+===== Example of Classes for Geometric Objects =====
|
|
|
+# #endif
|
|
|
+
|
|
|
+We introduce class `Shape` as superclass for all specialized objects
|
|
|
+in a figure. This class does not store any data, but provides a
|
|
|
+series of functions that add functionality to all the subclasses.
|
|
|
+This will be shown later.
|
|
|
+
|
|
|
+=== Simple Geometric Objects ===
|
|
|
+
|
|
|
+One simple subclass is `Rectangle`:
|
|
|
+!bc pycod
|
|
|
+class Rectangle(Shape):
|
|
|
+ def __init__(self, lower_left_corner, width, height):
|
|
|
+ p = lower_left_corner # short form
|
|
|
+ x = [p[0], p[0] + width,
|
|
|
+ p[0] + width, p[0], p[0]]
|
|
|
+ y = [p[1], p[1], p[1] + height,
|
|
|
+ p[1] + height, p[1]]
|
|
|
+ self.shapes = {'rectangle': Curve(x,y)}
|
|
|
+!ec
|
|
|
+Any subclass of `Shape` will have a constructor which takes
|
|
|
+geometric information about the shape of the object and
|
|
|
+creates a dictionary `self.shapes` with the shape built of
|
|
|
+simpler shapes. The most fundamental shape is `Curve`, which is
|
|
|
+just a collection of $(x,y)$ coordinates in two arrays `x` and `y`.
|
|
|
+Drawing the `Curve` object is a matter of plotting `y` versus `x`.
|
|
|
+
|
|
|
+The `Rectangle` class illustrates how the constructor takes information
|
|
|
+about the lower left corner, the width and the height, and
|
|
|
+creates coordinate arrays `x` and `y` consisting of the four corners,
|
|
|
+plus the first one repeated such that plotting `x` and `y` will
|
|
|
+form a closed four-sided rectangle. This construction procedure
|
|
|
+demands that the rectangle will always be aligned with the $x$ and
|
|
|
+$y$ axis. However, we may easily rotate the rectangle about
|
|
|
+any point once the object is constructed.
|
|
|
+
|
|
|
+Class `Line` constitutes a similar example:
|
|
|
+!bc pycod
|
|
|
+class Line(Shape):
|
|
|
+ def __init__(self, start, end):
|
|
|
+ x = [start[0], end[0]]
|
|
|
+ y = [start[1], end[1]]
|
|
|
+ self.shapes = {'line': Curve(x, y)}
|
|
|
+!ec
|
|
|
+Here we only need two points, the start and end point on the line.
|
|
|
+However, we may add some useful functionality, e.g., the ability
|
|
|
+to give an $x$ coordinate and have the class calculate the
|
|
|
+corresponding $y$ coordinate:
|
|
|
+!bc pycod
|
|
|
+ def __call__(self, x):
|
|
|
+ """Given x, return y on the line."""
|
|
|
+ x, y = self.shapes['line'].x, self.shapes['line'].y
|
|
|
+ self.a = (y[1] - y[0])/(x[1] - x[0])
|
|
|
+ self.b = y[0] - self.a*x[0]
|
|
|
+ return self.a*x + self.b
|
|
|
+!ec
|
|
|
+Unfortunately, this is too simplistic because vertical lines cannot
|
|
|
+be handled (infinte `self.a`). The source code of `Line` therefore
|
|
|
+provides a more general solution at the cost of significantly
|
|
|
+longer code with more tests.
|
|
|
+
|
|
|
+A circle gives us somewhat increased complexity. Again we represent
|
|
|
+the geometic object by a `Curve` object, but this time the `Curve`
|
|
|
+object needs to store a large number of points on the curve such
|
|
|
+that a plotting program produces a visually smooth curve.
|
|
|
+The points on the circle must be calculated manually in the constructor
|
|
|
+of class `Circle`. The formulas for points $(x,y)$ on a curve with radius
|
|
|
+$R$ and center at $(x_0, y_0)$ are given by
|
|
|
+!bt
|
|
|
+\begin{align*}
|
|
|
+x &= x_0 + R\cos (t),\\
|
|
|
+y &= y_0 + R\sin (t),
|
|
|
+\end{align*}
|
|
|
+!et
|
|
|
+where $t\in [0, 2\pi]$. A discrete set of $t$ values in this
|
|
|
+interval gives the corresponding set of $(x,y)$ coordinates on
|
|
|
+the circle. The user must specify the resolution, i.e., the number
|
|
|
+of $t$ values, or equivalently, points on the circle. The circle's
|
|
|
+radius and center must of course also be specified.
|
|
|
+
|
|
|
+We can write the `Circle` class as
|
|
|
+!bc pycod
|
|
|
+class Circle(Shape):
|
|
|
+ def __init__(self, center, radius, resolution=180):
|
|
|
+ self.center, self.radius = center, radius
|
|
|
+ self.resolution = resolution
|
|
|
+
|
|
|
+ t = linspace(0, 2*pi, resolution+1)
|
|
|
+ x0 = center[0]; y0 = center[1]
|
|
|
+ R = radius
|
|
|
+ x = x0 + R*cos(t)
|
|
|
+ y = y0 + R*sin(t)
|
|
|
+ self.shapes = {'circle': Curve(x, y)}
|
|
|
+!ec
|
|
|
+As in class `Line` we can offer the possibility to give an angle
|
|
|
+$\theta$ (equivalent to $t$ in the formulas above)
|
|
|
+and then get the corresponding $x$ and $y$ coordinates:
|
|
|
+!bc pycod
|
|
|
+ def __call__(self, theta):
|
|
|
+ """Return (x, y) point corresponding to angle theta."""
|
|
|
+ return self.center[0] + self.radius*cos(theta), \
|
|
|
+ self.center[1] + self.radius*sin(theta)
|
|
|
+!ec
|
|
|
+There is one flaw with this method: it yields illegal values after
|
|
|
+a translation, scaling, or rotation of the circle.
|
|
|
+
|
|
|
+A part of a circle, an arc, is a frequent geometric object when
|
|
|
+drawing mechanical systems. The arc is constructed much like
|
|
|
+a circle, but $t$ runs in $[\theta_0, \theta_1]$. Giving
|
|
|
+$\theta_1$ and $\theta_2$ the slightly more descriptive names
|
|
|
+`start_angle` and `arc_angle`, the code looks like this:
|
|
|
+!bc pycod
|
|
|
+class Arc(Shape):
|
|
|
+ def __init__(self, center, radius,
|
|
|
+ start_angle, arc_angle,
|
|
|
+ resolution=180):
|
|
|
+ self.center = center
|
|
|
+ self.radius = radius
|
|
|
+ self.start_angle = start_angle*pi/180 # radians
|
|
|
+ self.arc_angle = arc_angle*pi/180
|
|
|
+ self.resolution = resolution
|
|
|
+
|
|
|
+ t = linspace(self.start_angle,
|
|
|
+ self.start_angle + self.arc_angle,
|
|
|
+ resolution+1)
|
|
|
+ x0 = center[0]; y0 = center[1]
|
|
|
+ R = radius
|
|
|
+ x = x0 + R*cos(t)
|
|
|
+ y = y0 + R*sin(t)
|
|
|
+ self.shapes = {'arc': Curve(x, y)}
|
|
|
+!ec
|
|
|
+
|
|
|
+Having the `Arc` class, a `Circle` can alternatively befined as
|
|
|
+a subclass specializing the arc to a circle:
|
|
|
+!bc pycod
|
|
|
+class Circle(Arc):
|
|
|
+ def __init__(self, center, radius, resolution=180):
|
|
|
+ Arc.__init__(self, center, radius, 0, 360, resolution)
|
|
|
+!ec
|
|
|
+
|
|
|
+A wall is about drawing a curve, displacing the curve vertically by
|
|
|
+some thickness, and then filling the space between the curves
|
|
|
+by some pattern. The input is the `x` and `y` coordinate arrays
|
|
|
+of the curve and a thickness parameter. The computed coordinates
|
|
|
+will be a polygon: going along the originally curve and then back again
|
|
|
+along the vertically displaced curve. The relevant code becomes
|
|
|
+!bc pycod
|
|
|
+class CurveWall(Shape):
|
|
|
+ def __init__(self, x, y, thickness):
|
|
|
+ # User's curve
|
|
|
+ x1 = asarray(x, float)
|
|
|
+ y1 = asarray(y, float)
|
|
|
+ # Displaced curve (according to thickness)
|
|
|
+ x2 = x1
|
|
|
+ y2 = y1 + thickness
|
|
|
+ # Combine x1,y1 with x2,y2 reversed
|
|
|
+ from numpy import concatenate
|
|
|
+ x = concatenate((x1, x2[-1::-1]))
|
|
|
+ y = concatenate((y1, y2[-1::-1]))
|
|
|
+ wall = Curve(x, y)
|
|
|
+ wall.set_filled_curves(color='white', pattern='/')
|
|
|
+ self.shapes = {'wall': wall}
|
|
|
+!ec
|
|
|
+
|
|
|
+=== Class Curve ===
|
|
|
+
|
|
|
+Class `Curve` sits on the coordinates to be drawn, but how is
|
|
|
+that done? The constructor just stores the coordinates, while
|
|
|
+a method `draw` sends the coordinates to the plotting program
|
|
|
+to make a graph.
|
|
|
+Or more precisely, to avoid a lot of (e.g.) Matplotlib-specific
|
|
|
+plotting commands we have created a small layer with a
|
|
|
+simple programming interface to plotting programs. This makes it
|
|
|
+straightforward to change from Matplotlib to another plotting
|
|
|
+program. The programming interface is represented by the `drawing_tool`
|
|
|
+object and has a few functions:
|
|
|
+
|
|
|
+ * `plot_curve` for sending a curve in terms of $x$ and $y$ coordinates
|
|
|
+ to the plotting program,
|
|
|
+ * `set_coordinate_system` for specifying the graphics area,
|
|
|
+ * `erase` for deleting all elements of the graph,
|
|
|
+ * `set_grid` for turning on a grid (convenient while constructing the plot),
|
|
|
+ * `set_instruction_file` for creating a separate file with all
|
|
|
+ plotting commands (Matplotlib commands in our case),
|
|
|
+ * a series of `set_X` functions where `X` is some property like
|
|
|
+ `linecolor`, `linestyle`, `linewidth`, `filled_curves`.
|
|
|
+
|
|
|
+This is basically all we need to communicate to a plotting program.
|
|
|
+
|
|
|
+Any class in the `Shape` hierarchy inherits `set_X` functions for
|
|
|
+setting properties of curves. This information is propagated to
|
|
|
+all other shape objects that make up the figure. Class
|
|
|
+`Curve` stores the line properties together with the coordinates
|
|
|
+of its curve and propagates this information to the plotting program.
|
|
|
+When saying `vehicle.set_linewidth(10)`, all objects that make
|
|
|
+up the `vehicle` object will get a `set_linewidth(10)` call,
|
|
|
+but only the `Curve` object at the end of the chain will actually
|
|
|
+store the information and send it to the plotting program.
|
|
|
+
|
|
|
+A rough sketch of class `Curve` reads
|
|
|
+!bc pycod
|
|
|
+class Curve(Shape):
|
|
|
+ """General curve as a sequence of (x,y) coordintes."""
|
|
|
+ def __init__(self, x, y):
|
|
|
+ self.x = asarray(x, dtype=float)
|
|
|
+ self.y = asarray(y, dtype=float)
|
|
|
+
|
|
|
+ self.linestyle = None
|
|
|
+ self.linewidth = None
|
|
|
+ self.linecolor = None
|
|
|
+ self.fillcolor = None
|
|
|
+ self.fillpattern = None
|
|
|
+ self.arrow = None
|
|
|
+
|
|
|
+ def draw(self):
|
|
|
+ drawing_tool.plot_curve(
|
|
|
+ self.x, self.y,
|
|
|
+ self.linestyle, self.linewidth, self.linecolor,
|
|
|
+ self.arrow, self.fillcolor, self.fillpattern)
|
|
|
+
|
|
|
+ def set_linewidth(self, width):
|
|
|
+ self.linewidth = width
|
|
|
+
|
|
|
+ det set_linestyle(self, style):
|
|
|
+ self.linestyle = style
|
|
|
+ ...
|
|
|
+!ec
|
|
|
+
|
|
|
+=== Compound Geometric Objects ===
|
|
|
+
|
|
|
+The simple classes `Line`, `Arc`, and `Circle` could define the geometric
|
|
|
+shape through just one `Curve` object. More complicated figure elements
|
|
|
+are built from instances of various subclasses of `Shape`. Classes used
|
|
|
+for professional drawings soon get quite complex in composition and
|
|
|
+have a lot of geometric details, so here we prefer to make a very simple
|
|
|
+composition: the already drawy vehicle from
|
|
|
+Figure refref{sketcher:fig:vehicle0}.
|
|
|
+That is, instead of composing the drawing in a Python code we make a class
|
|
|
+`Vehicle0` for doing the same thing, and derive it from `Shape`.
|
|
|
+
|
|
|
+The `Shape` hierarchy is found in the `pysketcher` package, so to use these
|
|
|
+classes or derive a new one, we need to import `pysketcher`. The constructor
|
|
|
+of clas `Vehicle0` performs approximately the same statements as
|
|
|
+in the example program we developed for making the drawing in
|
|
|
+Figure refref{sketcher:fig:vehicle0}.
|
|
|
+!bc pycod
|
|
|
+class Vehicle0(Shape):
|
|
|
+ def __init__(self, w_1, R, L, H):
|
|
|
+ wheel1 = Circle(center=(w_1, R), radius=R)
|
|
|
+ wheel2 = wheel1.copy()
|
|
|
+ wheel2.translate((L,0))
|
|
|
+
|
|
|
+ under = Rectangle(lower_left_corner=(w_1-2*R, 2*R),
|
|
|
+ width=2*R + L + 2*R, height=H)
|
|
|
+ over = Rectangle(lower_left_corner=(w_1, 2*R + H),
|
|
|
+ width=2.5*R, height=1.25*H)
|
|
|
+
|
|
|
+ wheels = Composition(
|
|
|
+ {'wheel1': wheel1, 'wheel2': wheel2})
|
|
|
+ body = Composition(
|
|
|
+ {'under': under, 'over': over})
|
|
|
+
|
|
|
+ vehicle = Composition({'wheels': wheels, 'body': body})
|
|
|
+ xmax = w_1 + 2*L + 3*R
|
|
|
+ ground = Wall(x=[R, xmax], y=[0, 0], thickness=-0.3*R)
|
|
|
+
|
|
|
+ self.shapes = {'vehicle': vehicle, 'ground': ground}
|
|
|
+!ec
|
|
|
+
|
|
|
+Any subclass of `Shape` *must* define the `shapes` attribute, otherwise
|
|
|
+the inherited `draw` method (and a lot of other methods too) will
|
|
|
+not work.
|
|
|
+
|
|
|
+The painting of the vehicle could be offered by a method:
|
|
|
+!bc pycod
|
|
|
+ def colorful(self):
|
|
|
+ wheels = self.shapes['vehicle']['wheels']
|
|
|
+ wheels.set_filled_curves('blue')
|
|
|
+ wheels.set_linewidth(6)
|
|
|
+ wheels.set_linecolor('black')
|
|
|
+ under = self.shapes['vehicle']['body']['under']
|
|
|
+ under.set_filled_curves('red')
|
|
|
+ over = self.shapes['vehicle']['body']['over']
|
|
|
+ over.set_filled_curves(pattern='/')
|
|
|
+ over.set_linewidth(14)
|
|
|
+!ec
|
|
|
+
|
|
|
+The usage of the class is simple: after having set up an appropriate
|
|
|
+coordinate system a s previously shown, we can do
|
|
|
+!bc pycod
|
|
|
+vehicle = Vehicle0(w_1, R, L, H)
|
|
|
+vehicle.draw()
|
|
|
+drawing_tool.display()
|
|
|
+!ec
|
|
|
+The color from Figure ref{sketcher:fig:vehicle0:v2} is realized by
|
|
|
+!bc pycod
|
|
|
+drawing_tool.erase()
|
|
|
+vehicle.colorful()
|
|
|
+vehicle.draw()
|
|
|
+drawing_tool.display()
|
|
|
+!ec
|
|
|
+A complete code defining and using class `Vehicle0` is found in the file
|
|
|
+# #ifdef PRIMER_BOOK
|
|
|
+`vehicle2.py`.
|
|
|
+# #else
|
|
|
+"`vehicle2.py`": "http://hplgit.github.com/pysketcher/doc/src/sketcher/src-sketcher/vehicle2.py".
|
|
|
+# #endif
|
|
|
+
|
|
|
+The `pysketcher` package contains a wide range of classes for various
|
|
|
+geometrical objects, particularly those that are frequently used in
|
|
|
+drawings of mechanical systems.
|
|
|
+
|
|
|
+======= Adding Functionality via Recursion =======
|
|
|
+
|
|
|
+The really powerful feature of our class hierarchy is that we can add
|
|
|
+much functionality to the superclass `Shape` and to the "bottom" classe
|
|
|
+`Curve`, and all other classes for all types of geometrical shapes
|
|
|
+immediately get the new functionality. To explain the idea we first have
|
|
|
+to look at the `draw` method, which all classes in the `Shape`
|
|
|
+hierarchy must have. The inner workings of the `draw` method explain
|
|
|
+the secrets of how a series of other useful operations on figures
|
|
|
+can be implemented.
|
|
|
+
|
|
|
+=== Basic Principles of Recursion ===
|
|
|
+
|
|
|
+We work with two types of class hierarchies: one Python class hierarcy,
|
|
|
+with `Shape` as superclass, and one *object hierarchy* of figure elements
|
|
|
+in a specific figure. A subclass of `Shape` stres its figure in the
|
|
|
+`self.shapes` dictionary. This dictionary represents the object hierarchy
|
|
|
+of figure elements for that class. We want to make one `draw` call
|
|
|
+for an instance, say our class `Vehicle0`, and then we want this call
|
|
|
+to be propagated to *all* objects that are contained in
|
|
|
+`self.shapes` and all is nested subdictionaries. How is this done?
|
|
|
+
|
|
|
+The natural starting point is to call `draw` for each `Shape` object
|
|
|
+in the `self.shapes` dictionary:
|
|
|
+!bc pycod
|
|
|
+def draw(self):
|
|
|
+ for shape in self.shapes:
|
|
|
+ self.shapes[shape].draw()
|
|
|
+!ec
|
|
|
+This general method can be provided by class `Shape` and inherited in
|
|
|
+subclasses like `Vehicle0`. Let `v` be a `Vehicle0` instance.
|
|
|
+Seemingly, a call `v.draw()` just calls
|
|
|
+!bc pydoc
|
|
|
+v.shapes['vehicle'].draw()
|
|
|
+v.shapes['ground'].draw()
|
|
|
+!ec
|
|
|
+However, in the former call we call the `draw` method of a `Composition` object
|
|
|
+whose `self.shapes` attributed has two elements: `wheels` and `body`.
|
|
|
+Since class `Composition` inherits the same `draw` method, this method will
|
|
|
+run through `self.shapes` and call `wheels.draw()` and `body.draw()`.
|
|
|
+Now, the `wheels` object is also a `Composition` with the same `draw`
|
|
|
+method, which will run through the `shapes` dictionary, now containing
|
|
|
+the `wheel1` and and `wheel2` objects. The `wheel1` object is a `Circle`,
|
|
|
+so calling `wheel1.draw()` calls the `draw` method in class `Circle`,
|
|
|
+but this is the same `draw` method as shown above. This method will
|
|
|
+therefore traverse the circle's `shapes` dictionary, which we have seen
|
|
|
+consists of one `Curve` element.
|
|
|
+
|
|
|
+The `Curve` object holds the coordinates to be plotted so here `draw`
|
|
|
+really needs to do something "physical", namely send the coordinates to
|
|
|
+the plotting program. The `draw` method is outlined in the short listing
|
|
|
+of class `Curve` shown previously.
|
|
|
+
|
|
|
+We can go to any of the other shape objects that appear in the figure
|
|
|
+hierarchy and follow their `draw` calls in the similar way. Every time,
|
|
|
+a `draw` call will invoke a new `draw` call, until we eventually hit
|
|
|
+a `Curve` object in the "botton" of the figure hiearchy, and then that part
|
|
|
+of the figure is really plotted (or more precisesly, the coordinates
|
|
|
+are sent to a plotting programm).
|
|
|
+
|
|
|
+When a method calls itself, such as `draw` does, the calls are known as
|
|
|
+*recursive* and the programming principle is referred to as
|
|
|
+*recursion*. This technique is very often used to traverse hierarchical
|
|
|
+structures like the figure structures we work with here. Even though the
|
|
|
+hierarchy of objects building up a figure are of different types, they
|
|
|
+all inherit the same `draw` method and therefore exhibit the same
|
|
|
+behavior with respect to drawing. Only the `Curve` object has a different
|
|
|
+`draw` method, which does not lead to more recursion. Without this
|
|
|
+different `draw` method in class `Curve`, the repeated `draw` calls would
|
|
|
+go on forever.
|
|
|
+
|
|
|
+=== Explaining Recursion ===
|
|
|
+
|
|
|
+Understanding recursion is usually a challenge. To get a better idea of
|
|
|
+how recursion works, we have equipped class `Shape` with a method `recurse`
|
|
|
+which just visits all the objects in the `shapes` dictionary and prints
|
|
|
+out a message for each object.
|
|
|
+This feature allows us to trace the execution and see exactly where
|
|
|
+we are in the hierarchy and which objects that are visited.
|
|
|
+
|
|
|
+The `recurse` method is very similar to `draw`:
|
|
|
+!bc pydoc
|
|
|
+ def recurse(self, name, indent=0):
|
|
|
+ # print message where we are (name is where we come from)
|
|
|
+ for shape in self.shapes:
|
|
|
+ # print message about which object to visit
|
|
|
+ self.shapes[shape].recurse(indent+2, shape)
|
|
|
+!ec
|
|
|
+The `indent` parameter governs how much the message from this
|
|
|
+`recurse` method is intended. We increase `indent` by 2 for every level
|
|
|
+in the hierarchy. This makes it easy to see on the printout how far
|
|
|
+down in the hierarchy we are.
|
|
|
+
|
|
|
+A typical message written by `recurse` when `name` is `body` and
|
|
|
+the `shapes` dictionary contains two entries, `over` and `under`,
|
|
|
+will be
|
|
|
+!bc dat
|
|
|
+ Composition: body.shapes has entries 'over', 'under'
|
|
|
+ call body.shapes["over"].recurse("over", 6)
|
|
|
+!ec
|
|
|
+The number of leading blanks on each line corresponds to the value of
|
|
|
+`indent`. The code printing out such messages looks like
|
|
|
+!bc pycod
|
|
|
+ def recurse(self, name, indent=0):
|
|
|
+ space = ' '*indent
|
|
|
+ print space, '%s: %s.shapes has entries' % \
|
|
|
+ (self.__class__.__name__, name), \
|
|
|
+ str(list(self.shapes.keys()))[1:-1]
|
|
|
+
|
|
|
+ for shape in self.shapes:
|
|
|
+ print space,
|
|
|
+ print 'call %s.shapes["%s"].recurse("%s", %d)' % \
|
|
|
+ (name, shape, shape, indent+2)
|
|
|
+ self.shapes[shape].recurse(shape, indent+2)
|
|
|
+!ec
|
|
|
+
|
|
|
+Let us follow a `v.recurse('vehicle')` call in detail, `v` being
|
|
|
+a `Vehicle0` instance. Before looking into the output from `recurse`,
|
|
|
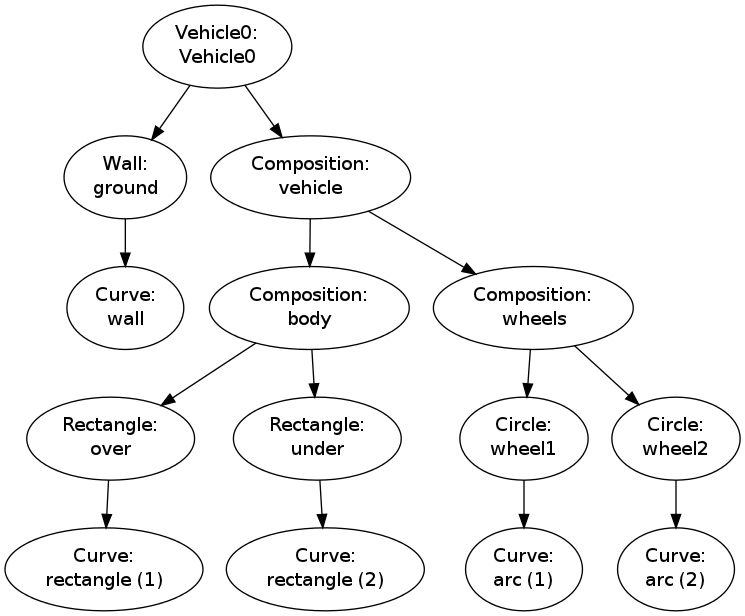
+let us get an overfiew of the figure hierarchy in the `v` object
|
|
|
+(as produced by `print v`)
|
|
|
+!bc dat
|
|
|
+ground
|
|
|
+ wall
|
|
|
+vehicle
|
|
|
+ body
|
|
|
+ over
|
|
|
+ rectangle
|
|
|
+ under
|
|
|
+ rectangle
|
|
|
+ wheels
|
|
|
+ wheel1
|
|
|
+ arc
|
|
|
+ wheel2
|
|
|
+ arc
|
|
|
+!ec
|
|
|
+The `recurse` method performs the same kind of traversal of the
|
|
|
+hierarchy, but writes out and explains a lot more.
|
|
|
+
|
|
|
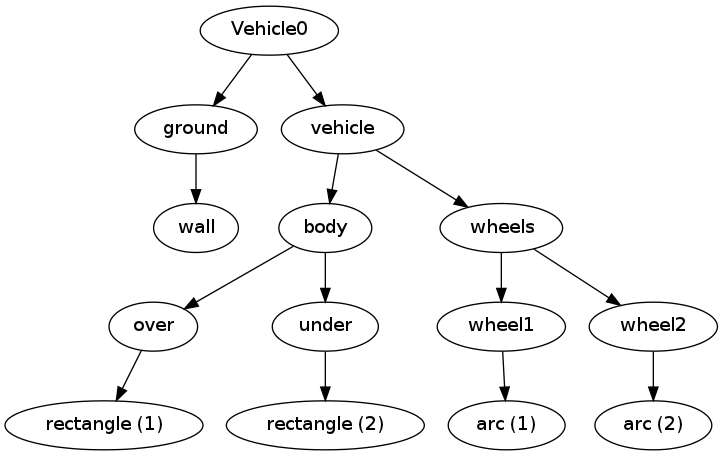
+The data structure represented by `v.shapes` is known as a *tree*.
|
|
|
+As in physical trees, there is a *root*, here the `v.shapes`
|
|
|
+dictionary. A graphical illustration of the tree (upside down) is
|
|
|
+shown in Figure ref{sketcher:fig:Vehicle0:hier2}.
|
|
|
+From the root there are one or more branches, here two:
|
|
|
+`ground` and `vehicle`. Following the `vehicle` branch, it has two new
|
|
|
+branches, `body` and `wheels`. Relationships as in family trees
|
|
|
+are often used to describe the relations in object trees too: we say
|
|
|
+that `vehicle` is the parent of `body` and that `body` is a child of
|
|
|
+`vehicle`. The term *node* is also often used to describe an element
|
|
|
+in a tree. A node may have several other nodes as *descendants*.
|
|
|
+
|
|
|
+FIGURE: [figs-sketcher/Vehicle0_hier2.png, width=600] Hierarchy of figure elements in an instance of class `Vehicle0`. label{sketcher:fig:Vehicle0:hier2}
|
|
|
+
|
|
|
+Recursion is the principal programming technique to traverse tree structures.
|
|
|
+Any object in the tree can be viewed as a root of a subtree. For
|
|
|
+example, `wheels` is the root of a subtree that branches into
|
|
|
+`wheel1` and `wheel2`. So when processing an object in the tree,
|
|
|
+we imagine we process the root and then recurse into a subtree, but the
|
|
|
+first object we recurse into can be viewed as the root of the subtree, so the
|
|
|
+processing procedure of the parent object can be repeated.
|
|
|
+
|
|
|
+A recommended next step is to simulate the `recurse` method by hand and
|
|
|
+carefully check that what happens in the visits to `recurse` is
|
|
|
+consistent with the output listed below. Although tedious, this is
|
|
|
+a major exercise that guaranteed will help to demystify recrusion.
|
|
|
+Also remember that it requires some efforts to understand recursion.
|
|
|
+
|
|
|
+A part of the printout of `v.recurse('vehicle')` looks like
|
|
|
+!bc dat
|
|
|
+ Vehicle0: vehicle.shapes has entries 'ground', 'vehicle'
|
|
|
+ call vehicle.shapes["ground"].recurse("ground", 2)
|
|
|
+ Wall: ground.shapes has entries 'wall'
|
|
|
+ call ground.shapes["wall"].recurse("wall", 4)
|
|
|
+ reached "bottom" object Curve
|
|
|
+ call vehicle.shapes["vehicle"].recurse("vehicle", 2)
|
|
|
+ Composition: vehicle.shapes has entries 'body', 'wheels'
|
|
|
+ call vehicle.shapes["body"].recurse("body", 4)
|
|
|
+ Composition: body.shapes has entries 'over', 'under'
|
|
|
+ call body.shapes["over"].recurse("over", 6)
|
|
|
+ Rectangle: over.shapes has entries 'rectangle'
|
|
|
+ call over.shapes["rectangle"].recurse("rectangle", 8)
|
|
|
+ reached "bottom" object Curve
|
|
|
+ call body.shapes["under"].recurse("under", 6)
|
|
|
+ Rectangle: under.shapes has entries 'rectangle'
|
|
|
+ call under.shapes["rectangle"].recurse("rectangle", 8)
|
|
|
+ reached "bottom" object Curve
|
|
|
+...
|
|
|
+!ec
|
|
|
+This example should clearly demonstrate the principle that we
|
|
|
+can start at any object in the tree and do a recursive set
|
|
|
+of calls with that object as root.
|
|
|
+
|
|
|
+
|
|
|
+===== Scaling, Translating, and Rotating a Figure =====
|
|
|
+label{sketcher:scaling}
|
|
|
+
|
|
|
+With recursion, as explained in the previous section, we can within
|
|
|
+minutes equip *all* classes in the `Shape` hierarchy, both present and
|
|
|
+future ones, with the ability to scale the figure, translate it,
|
|
|
+or rotate it. This added functionality requires only a few lines
|
|
|
+of code.
|
|
|
+
|
|
|
+=== Scaling ===
|
|
|
+
|
|
|
+We start with the simplest of the three geometric transformations,
|
|
|
+namely scaling.
|
|
|
+For a `Curve` instance containing a set of $n$ coordinates
|
|
|
+$(x_i,y_i)$ that make up a curve, scaling by
|
|
|
+a factor $a$ means that we multiply all the $x$ and $y$ coordinates
|
|
|
+by $a$:
|
|
|
+!bt
|
|
|
+\[
|
|
|
+x_i \leftarrow ax_i,\quad y_i\leftarrow ay_i,
|
|
|
+\quad i=0,\ldots,n-1\thinspace .
|
|
|
+\]
|
|
|
+!et
|
|
|
+Here we apply the arrow as an assignment operator.
|
|
|
+The corresponding Python implementation in
|
|
|
+class `Curve` reads
|
|
|
+!bc cod
|
|
|
+class Curve:
|
|
|
+ ...
|
|
|
+ def scale(self, factor):
|
|
|
+ self.x = factor*self.x
|
|
|
+ self.y = factor*self.y
|
|
|
+!ec
|
|
|
+Note here that `self.x` and `self.y` are Numerical Python arrays,
|
|
|
+so that multiplication by a scalar number `factor` is
|
|
|
+a vectorized operation.
|
|
|
+
|
|
|
+An even more efficient implementation is
|
|
|
+to make use of in-place multiplication in the arrays, as this saves the creation
|
|
|
+of temporary arrays like `factor*self.x`, which is then assigned to
|
|
|
+`self.x`:
|
|
|
+!bc cod
|
|
|
+class Curve:
|
|
|
+ ...
|
|
|
+ def scale(self, factor):
|
|
|
+ self.x *= factor
|
|
|
+ self.y *= factor
|
|
|
+!ec
|
|
|
+
|
|
|
+In an instance of a subclass of `Shape`,
|
|
|
+the meaning of a method `scale` is
|
|
|
+to run through all objects in the dictionary `shapes` and ask
|
|
|
+each object to scale itself. This is the same delegation of actions
|
|
|
+to subclass instances as we do in the `draw` (or `recurse`) method. All
|
|
|
+all objects, except `Curve` instances, can share the same
|
|
|
+implementation of the `scale` method. Therefore, we place
|
|
|
+the `scale` method in the superclass `Shape` such that all
|
|
|
+subclasses inherit the method.
|
|
|
+Since `scale` and `draw` are so similar,
|
|
|
+we can easily implement the `scale` method in class `Shape` by
|
|
|
+copying and editing the `draw` method:
|
|
|
+!bc cod
|
|
|
+class Shape:
|
|
|
+ ...
|
|
|
+ def scale(self, factor):
|
|
|
+ for shape in self.shapes:
|
|
|
+ self.shapes[shape].scale(factor)
|
|
|
+!ec
|
|
|
+This is all we have to do in order to equip all subclasses of
|
|
|
+`Shape` with scaling functionality!
|
|
|
+Any piece of the figure will scale itself, in the same manner
|
|
|
+as it can draw itself.
|
|
|
+
|
|
|
+
|
|
|
+=== Translation ===
|
|
|
+
|
|
|
+A set of coordinates $(x_i, y_i)$ can be translated $v_0$ units in
|
|
|
+the $x$ direction and $v_1$ units in the $y$ direction using the formulas
|
|
|
+!bt
|
|
|
+\begin{equation*}
|
|
|
+x_i\leftarrow x_i+v_0,\quad y_i\leftarrow y_i+v_1,\quad i=0,\ldots,n-1\thinspace . \end{equation*}
|
|
|
+!et
|
|
|
+The natural specification of the translation is in terms of a
|
|
|
+vector $v=(v_0,v_1)$.
|
|
|
+The corresponding Python implementation in class `Curve` becomes
|
|
|
+!bc cod
|
|
|
+class Curve:
|
|
|
+ ...
|
|
|
+ def translate(self, v):
|
|
|
+ self.x += v[0]
|
|
|
+ self.y += v[1]
|
|
|
+!ec
|
|
|
+The translation operation for a shape object is very similar to the
|
|
|
+scaling and drawing operations. This means that we can implement a
|
|
|
+common method `translate` in the superclass `Shape`. The code
|
|
|
+is parallel to the `scale` method:
|
|
|
+!bc cod
|
|
|
+class Shape:
|
|
|
+ ....
|
|
|
+ def translate(self, v):
|
|
|
+ for shape in self.shapes:
|
|
|
+ self.shapes[shape].translate(v)
|
|
|
+!ec
|
|
|
+
|
|
|
+=== Rotation ===
|
|
|
+
|
|
|
+Rotating a figure is more complicated than scaling and translating.
|
|
|
+A counter clockwise rotation of $\theta$ degrees for a set of
|
|
|
+coordinates $(x_i,y_i)$ is given by
|
|
|
+!bt
|
|
|
+\begin{align*}
|
|
|
+ \bar x_i &\leftarrow x_i\cos\theta - y_i\sin\theta,\\
|
|
|
+ \bar y_i &\leftarrow x_i\sin\theta + y_i\cos\theta\thinspace .
|
|
|
+\end{align*}
|
|
|
+!et
|
|
|
+This rotation is performed around the origin. If we want the figure
|
|
|
+to be rotated with respect to a general point $(x,y)$, we need to
|
|
|
+extend the formulas above:
|
|
|
+!bt
|
|
|
+\begin{align*}
|
|
|
+ \bar x_i &\leftarrow x + (x_i -x)\cos\theta - (y_i -y)\sin\theta,\\
|
|
|
+ \bar y_i &\leftarrow y + (x_i -x)\sin\theta + (y_i -y)\cos\theta\thinspace .
|
|
|
+\end{align*}
|
|
|
+!et
|
|
|
+The Python implementation in class `Curve`, assuming that $\theta$
|
|
|
+is given in degrees and not in radians, becomes
|
|
|
+!bc cod
|
|
|
+ def rotate(self, angle, center):
|
|
|
+ angle = radians(angle)
|
|
|
+ x, y = center
|
|
|
+ c = cos(angle); s = sin(angle)
|
|
|
+ xnew = x + (self.x - x)*c - (self.y - y)*s
|
|
|
+ ynew = y + (self.x - x)*s + (self.y - y)*c
|
|
|
+ self.x = xnew
|
|
|
+ self.y = ynew
|
|
|
+!ec
|
|
|
+The `rotate` method in class `Shape` is identical to the
|
|
|
+`draw`, `scale`, and `translate` methods except that we
|
|
|
+recurse into `self.rotate(angle, center)`.
|
|
|
+
|
|
|
+We have already seen the `rotate` method in action when animating the
|
|
|
+rolling wheel at the end of Section ref{sketcher:vehicle1:anim}.
|